
#RIPPLE CARRY ADDER TRUTH TABLE FULL#
1 bit full adder schematic and truth tableĪ Full adder can be made by combining two half adder circuits together (a half adder is a circuit that adds two input bits and outputs a sum bit and a carry bit). This can be applied to any row in the table. 2 in the decimal system corresponds to 10 in the binary system. Swapping the result “10” will give S=0 and Cout = 1 and the second last row is justified. and so the result of 1+1+0 is 10 just like we get 1+1+0 =2 in decimal system.

In binary system, the number order is 0, 1, 10, 11……. Consider the second last row of the truth table, here the operands are 1, 1, 0 ie (A, B, Cin). Add them together ie 1+1+0 = 10. There is a simple trick to find results of a full adder. Truth table and schematic of a 1 bit Full adder is shown below The Sum out (Sout) of a full adder is the XOR of input operand bits A, B and the Carry in (Cin) bit.
#RIPPLE CARRY ADDER TRUTH TABLE PLUS#
Full adder is a logic circuit that adds two input operand bits plus a Carry in bit and outputs a Carry out bit and a sum bit. To understand the working of a ripple carry adder completely, you need to have a look at the full adder too. In simple words, the final result of the ripple carry adder is valid only after the joint propogation delays of all full adder circuits inside it. In the same way, Sum out S3 of the Full Adder 4 is valid only after the joint propagation delays of Full Adder 1 to Full Adder 4. Sum out S0 and carry out Cout of the Full Adder 1 is valid only after the propagation delay of Full Adder 1. Circuit diagram of a 4-bit ripple carry adder is shown below. Similarly the carry propagation delay is the time elapsed between the application of the carry in signal and the occurance of the carry out (Cout) signal. The time taken for the NOT gate’s output to become “0” after the application of logic “1” to the NOT gate’s input is the propagation delay here. Consider a NOT gate, When the input is “0” the output will be “1” and vice versa.
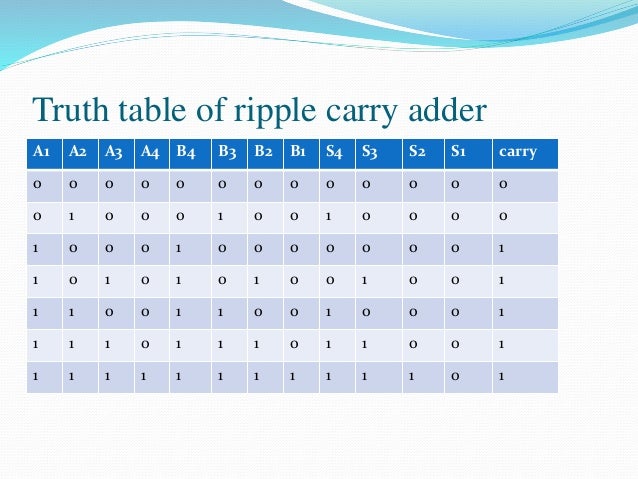

Propagation delay is time elapsed between the application of an input and occurance of the corresponding output. In a ripple carry adder the sum and carry out bits of any half adder stage is not valid until the carry in of that stage occurs.Propagation delays inside the logic circuitry is the reason behind this. It is called a ripple carry adder because each carry bit gets rippled into the next stage. A ripple carry adder is a logic circuit in which the carry-out of each full adder is the carry in of the succeeding next most significant full adder. For an N- bit parallel adder, there must be N number of full adder circuits. Multiple full adder circuits can be cascaded in parallel to add an N-bit number. A ripple carry adder is an important digital electronics concept, essential in designing digital circuits. In this article, learn about Ripple carry adder by learning the circuit.


 0 kommentar(er)
0 kommentar(er)
